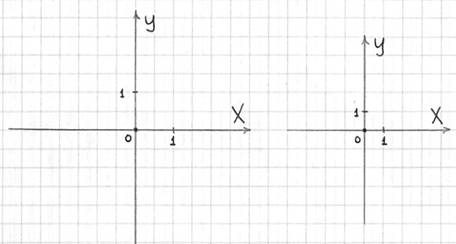
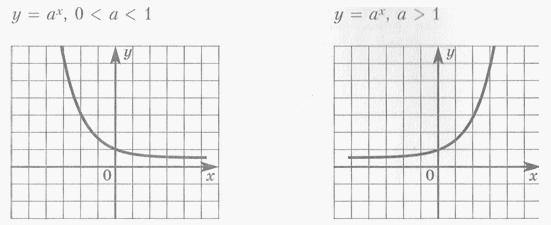
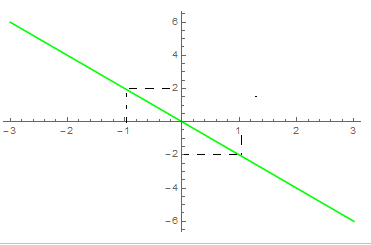
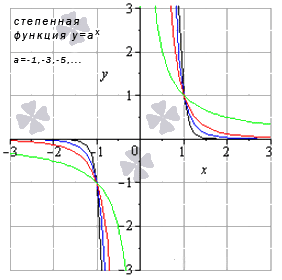
Понятие функции и способы ее задания
Для всех перечисленных числовых множеств, кроме комплексных чисел, определено также отношение линейного порядка , позволяющее сравнивать числа по величине. Числовые пространства — это числовые множества вместе с функцией расстояния , заданной на соответствующем множестве. В самом общем случае, числовая функция — это функция, принимающая значения в области вещественных чисел и которая задана на произвольном чаще всего метрическом пространстве. Такова, например, индикаторная или характеристическая функция множества. Другой пример числовой функции — это функция расстояния или, что то же самое, метрика. Числовые функции , заданные на множестве вещественных или комплексных чисел называются функциями соответственно вещественного или комплексного переменного и являются предметом рассмотрения в анализе :.
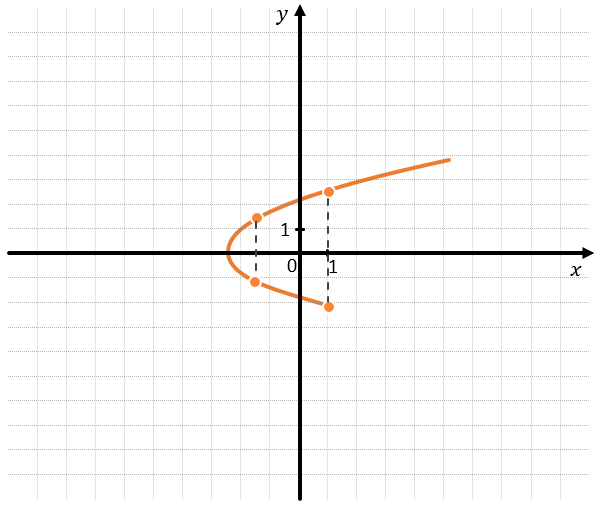

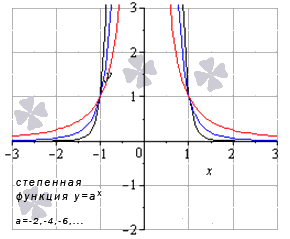
Категория: Математика. Похожие презентации:. Основные элементарные функции, их свойства и графики. Основные характеристики функции. Чётность функции. Основные понятия.
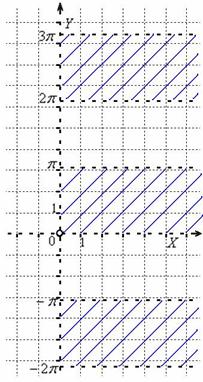




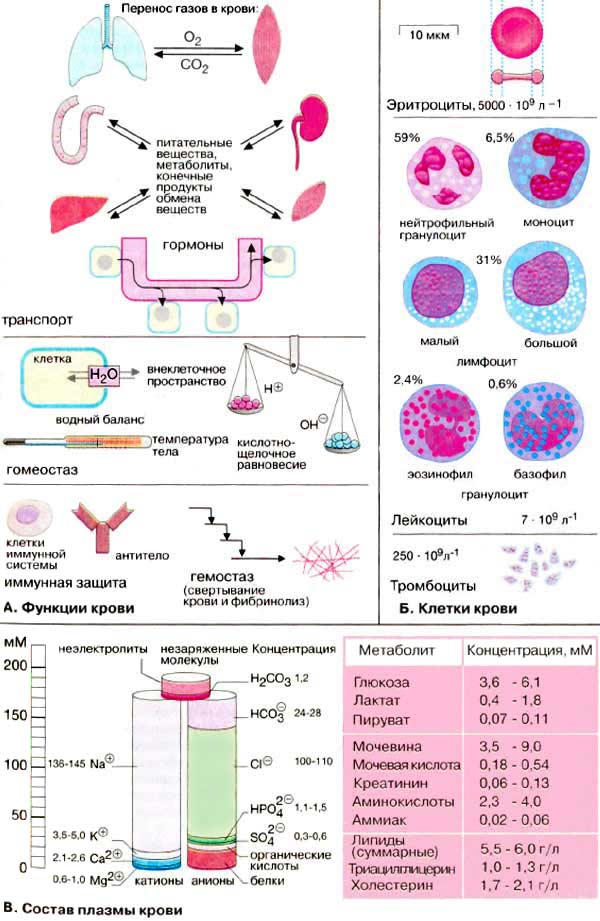
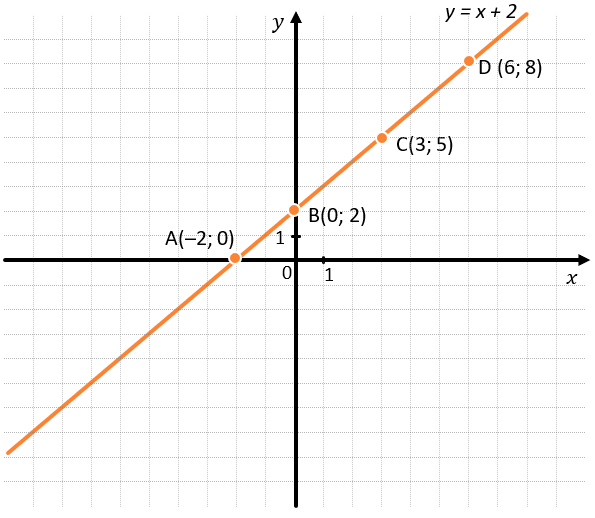
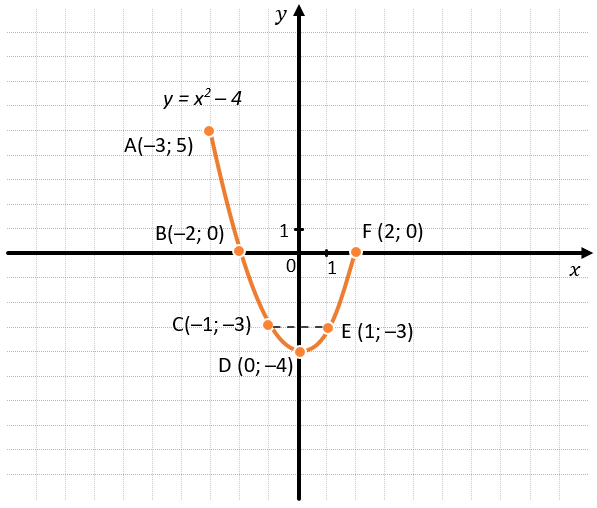
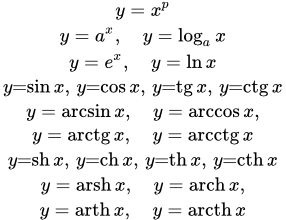
Чтобы понять суть функции, можно рассмотреть формулу периметра квадрата. Мы можем сами подставить любую длину стороны квадрата, чтобы получить соответствующий ей периметр. Если между двумя какими-либо величинами есть такое соответствие, то между ними существует функция. Мы говорим, что чтобы получить периметр квадрата, нужно его сторону умножить на 4. Это будет верно для любой стороны квадрата, которую мы сами зададим.